InfoVAE : Balancing Learning and Inference in Variational Autoencoder
2018 / arXiv.org / Shengjia Zhao, Jiaming Song, Stefano Ermon
지난 몇년간 ML 분야에서는 VAE(Variational Autoencoder)와 GAN(Generative Adversarial Network)를 필두로 generative model에 대한 연구가 활발하게 진행되었다.
이번에 살펴본 논문은
InfoVAE : Balancing Learning and Inference in Variational Autoencoder; Shengjia Zhao et al. 으로,
VAE의 목적 함수인 ELBO(Evidence Lower BOund)가 갖는 단점들을 분석하여 새로운 형태의 목적 함수를 제시하고 실험을 통해 결과를 살펴보았다.
1. Backgrounds
Generative model은 neural network (NN)를 통해 데이터의 확률 분포 자체를 학습하는 모델로, 그 예로 GAN, VAE 등이 있다.
주요 목표는 데이터 $x$의 분포와 $x$를 잘 설명하는 latent variable $z$의 분포를 학습하는 것이다. 하지만 VAE에서 사용되는 ELBO는 위의 두 목표가 상충될 때, $x$의 분포를 학습하는데 좀 더 중점을 두는 문제점이 있다. (결국 $z$와 $x$가 연관성이 떨어지는 문제가 발생할 수 있다.)
2. Variational Autoencoder
VAE와 목적함수 ELBO에 대해 간략하게 살펴보면 다음과 같다.
- Input variable : $x \in X$
- Latent variable : $z \in Z$
- Data distribution conditioned over $z$ : $p_{\theta}(x\mid z)$
- Prior distribution : $p(z)$
- True underlying distribution : $p_D (x)$
Generative model의 기본적인 목적은 다음의 likelihood를 최대화 하는 것을 볼 수 있다.
\[\mathbb{E}_{P_D(x)}[\log p_\theta(x)]=\mathbb{E}_{p_D(x)}[\log\mathbb{E}_{p(z)}[p_\theta(x\mid z )]] \tag{1}\]그러나 $p_\theta(x)=\int_z p_\theta(x\mid z)p(z)dz$가 intractable하므로 $q_\phi(z\mid x)$를 통해 위 식의 lower bound를 maximize하는 방법으로 돌려서 풀게된다.
결과적으로 VAE에서 사용되는 ELBO는 다음과 같다.
\[\mathcal{L}_{ELBO}=\mathbb{E}_{p_D(x)}[-D_{KL}(q_\phi(z\mid x)\parallel p(z))+\mathbb{E}_{q_\phi(z\mid x)}[\log p_\theta(x\mid z )]]\leq\mathbb{E}_{p_D(x)}[\log p_\theta(x)]\]또한 $p_\theta(x,z) \equiv p(z)p_\theta(x\mid z), q_\phi(x,z)\equiv p_D(x)q_\phi(z\mid x)$로 정의하면 ELBO는 다음의 식으로 변형 될 수 있다.
\(\mathcal{L}_{ELBO}\equiv -D_{KL}(q_\phi(x,z)\parallel p_\theta(x,z))\tag{2}\) \(=-D_{KL}(p_D(x)\parallel p_\theta(x))-\mathbb{E}_{p_D(x)}[D_{KL}(q_\phi(z\mid x)\parallel p_\theta(z\mid x))]\tag{3}\) \(=-D_{KL}(q_\phi(z)\parallel p(z))-\mathbb{E}_{q_\phi(z)}[D_{KL}(q_\phi(x\mid z)\parallel p_\theta(x\mid z))]\tag{4}\)
3. Two problems of VAE
3.1. Amortized inference failures
이상적인 조건 하에서, ELBO 최적화는 위의 두가지 목표를 달성 할 수 있다 (with sufficiently flexible model families for $p_\theta(x\mid z)$ and $q_\phi(z\mid x)$ over $\theta , \phi$).
- Capturing $p_D(x)$
- Performing correct amortized inference $q_\phi(z\mid x)$
이는 Eq.(3)를 통해 확인 할 수 있는데, ELBO 최적화는 결국
- $p_D(x)$과 $p_\theta(x)$; data distribution과 model distribution
- $q_\phi(z\mid x)$와 $p_\theta(z\mid x)$; varitational posterior과 true posterior
의 KL Divergence를 최소화하는 것이기때문이다 (각각은 위의 1,2 목표와 동일).
하지만 finite model capacity로 인해 두가지 목표 사이에 trade-off가 발생하는 경우, $q_\phi(z\mid x)$의 학습이 희생되는 경향이 있는데, 논문에서는 그 이유를 두 가지로 설명하고있다.
- Inherent properties of the ELBO objective :
ELBO가 매우 부정확한 $q_\phi(z\mid x)$를 갖더라도 최대화가 가능. - Implicit modeling bias : $x$의 차원이 $z$에 비해 높기때문에, 최적화 수행 시 data fitting에 바이어스 됨.
3.1.1 Good ELBO values do not imply accurate inference
ELBO를 재구성하면 log likelihood (reconstruction) term인 \(\mathcal{L}_{\text{AE}}\) 와 regularization term \(\mathcal{L}_{\text{REG}}\)로 구성되어있는 것을 알 수 있다.
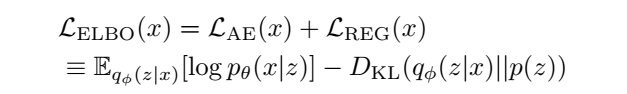
먼저 reconstruction term인 \(\mathcal{L}_{AE}\)만 최적화하는 경우를 살펴보면, inferred latent variable $z\sim q_\phi(z\mid x)$로부터 observing data point $x$의 log likelihood를 최대화하게 된다. 유한한 데이터 셋 ${x_1,…,x_N}$으로부터, $q_\phi$가 $x_i \neq x_j$일때 $q_\phi(z\mid x_i)$와 $q_\phi(z\mid x_j)$가 disjoint support를 갖는 distribution이라하면, $p_\theta(x\mid z )$는 각각의 $q_\phi(z\mid x_i)$로부터 학습 할 때 $x_i$로 집중되어있는 형태의 분포를 배운다는 것이다. 이로인해 $p_\theta(x\mid z )$는 Dirac delta distribution를 따라가는 경향이 발생하기도하는데, 부적절한 $z$를 학습하는데도 불구하고 \(\mathcal{L}_{AE}\)는 $+\infty$로 간다.
논문에서는 간단한 예시로 $x\in {-1,1}$인 경우, true prior $p(z)$와 $q_\phi(z\mid x)$의 모델링에 대해 살펴보았다. $x=\pm1$로 conditioned되어있을 때 $q_phi$의 평균과 분산이 각각 $\pm\infty,+0$인 경우 \(\mathcal{L}_{ELBO}\)가 $+\infty$로 최대화되는 것을 증명하였다 (이때 $q_\phi(z\mid x)$와 $p_\theta(z\mid x)$의 KL divergence 또한 $+\infty$가 된다).
즉 ELBO를 최대화하는 쪽으로 잘 학습함에도 불구하고, 쓸모없는 inference $q_\phi(z)$를 (ture posterior와 상관없는)를 얻는다는 것이다.
3.1.2 Modeling bias
두번째 문제는 modeling bias로 ELBO에 $x$와 $z$에 대한 요소가 모두 존재하지만 $x$에 대한 error term이 더 dominant하다는 것이다.
예를들어, 두 $n$-dimensional Gaussian distribution $\mathcal{N}(0,I), \mathcal{N}(\epsilon,I)$의 KL-divergence는 아래와 같다.
\[D_{KL}(\mathcal{N}(0,I), \mathcal{N}(\epsilon,I))=n\epsilon^2/2\]보통 $x$가 $z$에 비해 고차원이기 때문에, $x$의 오차를 줄이는 것이 더 효과적이기때문에, $z$가 희생되는 경향이 생긴다. 나아가 이러한 문제는 아래 현상의 원인이 될 수 있다.
- Inference 성능의 약화
- 트레이닝 데이터에 대한 오버피팅
3.2. The information preference propoerty
PixelRNN/PixelCNN과 같은 복잡한 $p_\theta(x\mid z )$ 복원 방법들은 natural image dataset의 샘플 퀄리티를 크게 향상시켰으나, latent variable $z$를 무시하는 새로운 문제($x$와 $z$의 mutual information이 굉장히 작아지게되는) 문제가 발생하게 되었다. 직관적인 원인은 $z$에 상관없이 학습된 $p_\theta(x\mid z )$가 동일하다는 것인데, 의미있는 latent variable을 찾는 목적 달성이 전혀 이뤄지지 않게 되는 것이다.
논문에서는 이러한 현상을 information preference problem이라 하며, 이와 연관해서 ELBO에 대한 다음과 같은 해석을 내놓았다. 요약하면 latent variable $z$을 활용하지 않더라도도 0으로 최적화가 가능하다는 것이다.
ELBO의 재구성 식인 (3)을 보면 $-D_{KL}(p_D(x)\parallel p_\theta(x))$과 \(-\mathbb{E}_{p_D(x)}[D_{KL}(q_\phi(z\mid x)\parallel p_\theta(z\mid x))]\) 두 가지 term으로 구성되어있는데 다음을 통해 $x$와 $z$ 사이의 연관성이 없어도 global optimum을 얻는 것을 보였다.

4. The InfoVAE model family
위의 두 문제 (3.1,3.2)를 해결하기위해 새로운 학습 목적함수를 제안했다. 즉 원래 ELBO 수식으로부터
1) Scaling parameter $\lambda$를 통한 $x$에 편중되는 문제 해결 (3.1)
2) Mutual information maximization term을 추가하여 $x,z$ 사이의 연관성 문제를 해결 (3.2)
따라서 새로운 목적함수는
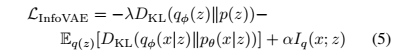
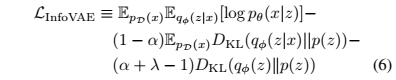
(5)와 (6)은 동일한 수식인데, (6)의 경우 효율적인 최적화가 가능하다고 한다. (6)의 마지막 $D_{KL}(q_\phi(z)\parallel p(z))$ term 계산에서 어려움이 있을 수 있는데 ($\log q_\phi(z)$ 파트), unbiased sampling이 가능하여 lieklihood free optimization technique을 활용 할 수 있다. 나아가 다음의 조건에서 KL-divergence 외에 다른 strict divergence $D(q_\phi(z)\parallel p(z))$를 사용한 목적함수 $\hat{\mathcal{L}}_{\text{infoVAE}}$로 교체하더라도 최적화에 전혀 문제가 되지 않음을 보였다.
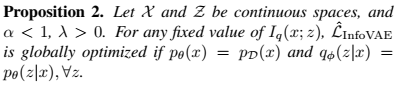
${\mathcal{L}}_{\text{infoVAE}}$은 이전에 발표된 여러 모델의 일반화된 버전으로 볼 수 있다. 예를들어
- $\alpha=0, \lambda=1$ : 기존 ELBO 모델
- $\lambda>0, \alpha+\lambda-1=0$, KL-divergence : $\beta$-VAE.
- $\alpha=1,\lambda=1$, Jensen Shannon divergence : Adversarial Autoencoder
4.1 Divergence families
Proposition 2를 통해 KL-divergence외에 다른 divergence의 사용이 가능하므로, 논문에서 3가지 divergence에 대해 고려했다.
- Adversarial training : Adversarial Autoencoder (AAE)에서 Adversarial discriminator를 통해 $q_\phi(z)$와 $p(z)$사이의 Jensen-Shannon divergence를 approximately 최소화.
- Stein Variational Gradient : KL-divergence의 Gradient를 계산해서 $D_{KL}$에 대한 gradient discent minimization 수행.
- Maximum-Mean discrepancy : 두 분포의 moment를 통해 거리 수치화.
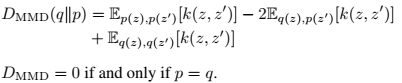
5. Experiments
시뮬레이션을 통해서 논문에서 전개한 이론적인 측면을 확인한다.
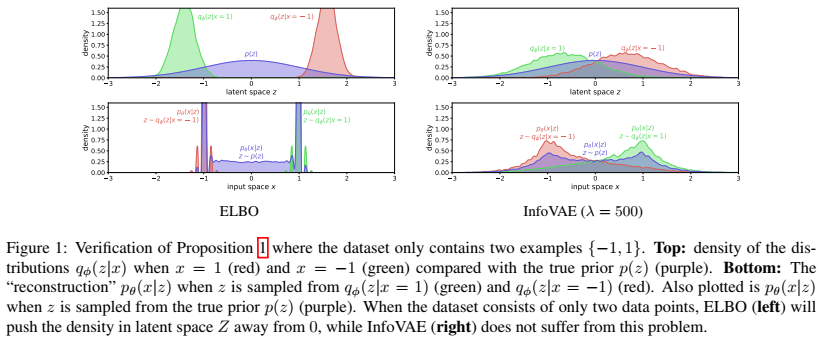
$x$가 -1 혹은 1 값을 갖는 경우에 대한 간단한 시뮬레이션인데, 기존 ELBO objective에서 $p(z)$와 $q_\phi(z\mid x)$ 사이의 $D_{KL}$ term이 존재하지만 그래프를 살펴보면 $p(z)$와 $q_\phi(z\mid x)$의 형태가 다른 것을 확인 할 수 있다. 반면에 InfoVAE의 경우 이러한 문제를 극복한 것을 확인 할 수 있다.
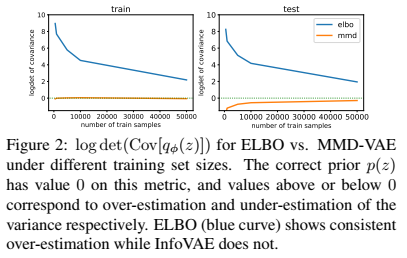
이 그래프는 ELBO의 over/under estimation에 관한 그래프로서, $\log \text{det(Cov}[q_\phi(z)])$를 training, test set에 대해 도시하였다. standard Gaussian prior $p(z)$의 $\text{Cov}[p(z)]=I$이므로 $\log \text{det(Cov}[p(z)])=0$이다. ELBO의 경우 ideal case와 큰 차이가 나타나는 것을 확인 할 수 있다. 특히 training set이 작을때 이러한 현상이 두드러진다. 반면에 MMD를 사용한 InfoVAE의 경우 이러한 문제가 나타나지 않는 것을 볼 수 있다.

위 그림은 500개로 트레이닝 했을때 $p(z), q_\phi(z)$의 contour이다. InfoVAE의 경우 prior와 유사한 분포를 갖는 반면에, ELBO는 동떨어진 결과를 나타내고, 결국 이는 Fig. 2에서 ELBO의 overestimation을 의미한다.

MNIST 데이터셋에 대한 VAE와 InfoVAE의 reconstruciton, generation 이미지이다. 상단은 ELBO 그래프인데, sharp한 reconstruction들을 생성하지만 generation 성능이 상당히 나쁜 것을 볼 수 있다. 따라서 복원 오차를 줄이는데에 generalization 성능 (learning good prior $z$)이 희생 된 것으로 보인다. 반면에 하단의 InfoVAE결과는 reconstruciton과 generation 결과 모두 숫자에 근접한 이미지들이 생성되는 것을 확인 할 수 있다.
요약
- Generative model에서는 sample generation도 중요하지만 잘 설명이 되는 latent variable $z$의 학습도 매우 중요하다.
- 하지만 기존 ELBO objective는 크게 두가지 한계를 내포하고 있는데, 첫번째로 $z$의 학습보다 $x$의 reconstruciton에 더 영향을 받는다는 것이고 두번째는 $x$와 $z$의 의미적인 연결에 문제가 있다는 것이다.
- 따라서 ELBO 내에서 $z$에 대한 웨이트를 주고 $x,z$ 사이의 mutual information에 보상을 줘서 두가지 문제를 해결한다.
- 결과적으로 InfoVAE를 통해서 기존 VAE보다 발전된 샘플을 얻으면서 latent variable $z$의 학습도 잘 이루어졌다.

댓글남기기