[Machine Learning] 인공신경망의 오버 피팅과 Regularization의 이해

Overfitting in Artificial Neural Networks

머신러닝, 인공신경망에서 필수적으로 알아야 할 개념 중 하나가 오버 피팅 (overfitting, 과적합)이다. 인터넷을 조금만 검색해보면 오버 피팅과 이를 방지하기위한 Regularization 방법에 관한 수 많은 포스트들이 있는데, 대부분 아래와 같은 두 가지 그림 중 하나를 사용하여 설명한다.

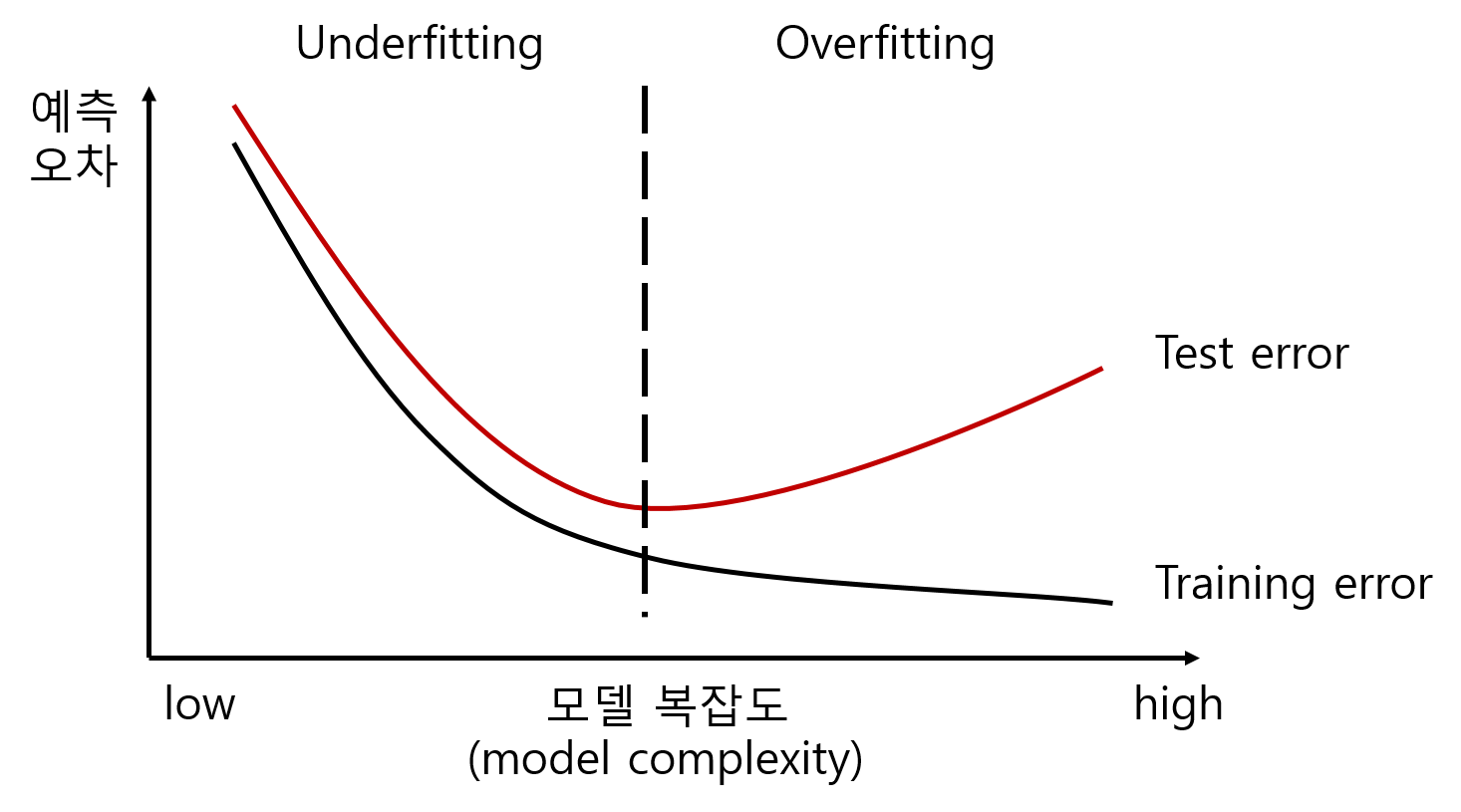
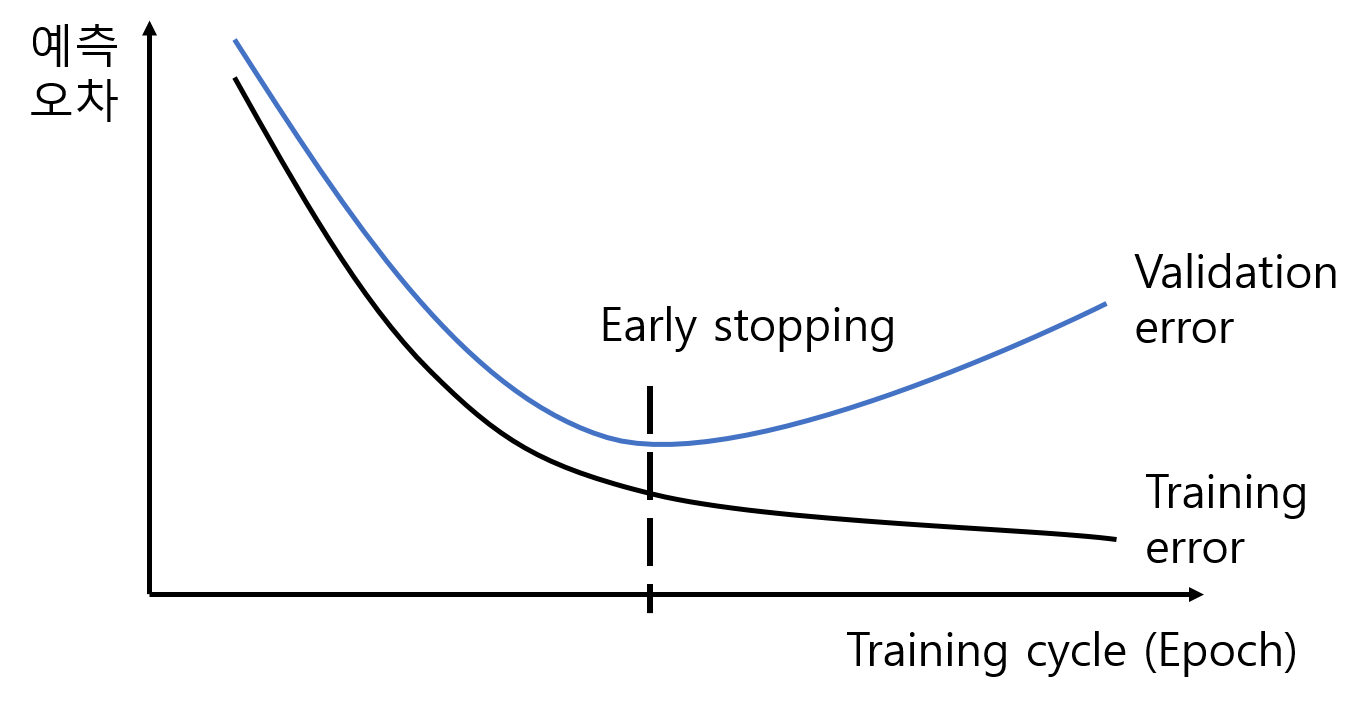
model complexity와 오버 피팅	training epoch과 오버피팅

간혹 인공 신경망의 오버 피팅은 보통 우측의 그림과 함께 인공 신경망의 학습이 너무 과하게 이루어져서 발생한다는 설명과 함께 이를 방지하기 위한 early stopping (학습 조기 종료) 방법에 대해 설명한다. 또, 기계 학습 관점에서 보면 오버 피팅의 발생은 모델 복잡도에 따라 나타나는 좌측의 그림으로 설명하면서 L1/L2 regularization을 소개하기도한다. 하지만 유사한 두개의 그래프를 연결시켜 설명하는 글은 거의 본 적이 없다. (early stopping과 L1/L2 regularization도 마찬가지) 이 포스트는 오버 피팅과 L1/L2 regularization, early stopping에 대한 개인적인 해석을 담고 있다.

1. 오버 피팅이란?

먼저 모델 학습을 위한 트레이닝 데이터를 $X_{train}$, 모델 테스트를 위한 테스트 데이터를 $X_{test}$라 한다. 각각의 데이터에 대한 모델의 오차를 계산할 수 있으므로 트레이닝 에러 $E_{train}$와 테스트 에러 $E_{test}$ 발생한다.

학습은 개인의 한정된 경험에 기반한다. 이는 기계 학습도 마찬가지다. 트레이닝 데이터 는 우리가 모르는 원래의 어떤 모델로부터 생성된 데이터들을 샘플링한 일부 의 데이터에 해당한다. 따라서 트레이닝 에러 와 테스트 에러 를 각각 in sample error, out of sample error 라고도 한다.

기계 학습의 목적은 트레이닝 에러와 테스트 에러가 모두 낮은 모델을 학습 하는 것이다. 학습의 진행, 즉 epoch이 증가함에 따라서 트레이닝 에러와 테스트 에러를 비교해보면 일반적으로 다음의 세가지 상황이 발생한다.

1. $E_{train}$ : 높음, $E_{test}$ : 높음
2. $E_{train}$ : 낮음, $E_{test}$ : 낮음
3. $E_{train}$ : 매우 낮음, $E_{test}$ : 높음

먼저 1번은 배운 문제도 잘 풀지 못하고 (high in sample error) 새로운 문제도 못푸는 (high out of sample error) 상황이다. 이러한 상황을 언더 피팅 (underfitting; 과소적합)이라 한다. 이 경우 모델이 뭘 배웠다고 말할 수 있는 상황이 아니므로 모델의 한계가 있는 것이거나 학습을 더 진행해야 하는 상황이다. 다음으로 2번의 경우가 배운 것도 잘하고 (low in sample error) 새 문제도 잘푸는 (low out of sample error) 케이스로 우리는 기계 학습을 통해 이러한 결과를 갖는 모델을 학습하기를 원한다. 마지막으로 3번은 배운 문제는 굉장히 잘 푸는데 (low in sample error) 오히려 새로운 문제는 못 푸는 (high out of sample error) 상황이다. “테스트 셋에만 적합”한 모델이기 때문에 이를 과적합, 즉 오버 피팅 (overfitting; 과적합)이라 한다. 물론 테스트 데이터는 학습에 사용되지 않았기 때문에 $E_{test}\geq E_{train}$인 상황이 정상적 이지만 오버 피팅은 $E_{train}$과 $E_{test}$의 그 차이의 정도가 심하다는 것이다. 즉, 모델이 트레이닝 데이터를 과도하게 학습한 나머지 트레이닝 에러는 매우 낮지만 테스트 에러는 오히려 더 증가하는 상태이다. 따라서 오버 피팅된 모델은 일반화 성능을 나타내는 테스트 에러가 높기 때문에 실사용에 적합하지 않으며, 오버 피팅의 발생을 방지하는 것이 매우 중요하다.

오버피팅 : 모델의 트레이닝 에러가 매우 낮은데 비해 테스트 에러가 비정상적으로 높은 상태

기출 문제는 100점 받는데 시험 점수는 6~70점 정도인 상황.

2. 오버 피팅이 발생하는 원인

오버 피팅이 발생하는 원인은 무엇일까?

일반적으로 높은 모델 복잡도 를 원인으로 보지만, 그전에 살펴봐야 할 점은 바로 학습 데이터가 충분한가 이다. 극단적으로 학습한 데이터가 발생 할 수 있는 데이터의 전부라면 트레이닝 에러 뿐만아니라 테스트 에러도 낮을 것이 자명하다. 그러나 대부분의 상황에서 발생 가능한 모든 데이터를 수집하는것은 불가능하므로 우리는 한정된 데이터 를 통해 학습도 잘하고 새로운 문제도 잘 해결하는 모델을 찾아야 하는 것이다. 그 한정된 데이터가 어떤 모델을 설명하기에 충분히 많다면 오버 피팅은 발생하지 않는데, 충분하지 않은 경우 이제 모델 복잡도 와 오버 피팅의 발생이 연결되는 것이다.

오버 피팅 발생의 근본적인 원인은 학습 데이터의 부족이다.

따라서 근본적인 해결책은 데이터를 충분히, 더 많이 모으는 것이다.

하지만 우리는 학습하려는 실제 모델을 모르기때문에 어느정도의 데이터가 충분 한 것인지 알 수 없다. 따라서 수집한 데이터 안에서 최대한 오버 피팅을 피하면서 일반화 성능이 좋은 모델을 개발해야한다. 이러한 상황으로부터 모델 복잡도 와 오버피팅의 상관성을 살펴볼 수 있다. 모델 복잡도란 간단하게 말해서 어떤 모델을 정의하기 위해 필요한 파라미터의 수로 생각할 수 있다. 즉 파라미터의 수가 많을수록 정교하고 복잡한 모델을 표현 할 수 있고, 적으면 간단한 모델만 설명할 수 있는 것이다. 모델 복잡도에 따라 발생하는 언더 피팅 오버 피팅의 그래프를 그려보면 다음과 같다.

모델 복잡도와 오버 피팅 그래프

그래프를 보면 낮은 모델 복잡도에서는 트레이닝 에러와 테스트 에러 모두 높게 나오는데, 일정 수준까지는 모델 복잡도가 증가할수록 트레이닝 에러와 테스트 에러가 모두 감소하는 것을 볼 수 있다. 반면에 모델 복잡도가 일정 수준을 넘어가게 되면 트레이닝 에러는 지속적으로 감소하는데비해서 오히려 테스트 에러가 증가하게 된다. 이러한 상태가 오버 피팅이고 트레이닝 데이터를 통해 어떠한 관계를 학습 한것이 아니고 데이터 자체를 암기 해버린 것으로 설명하기도 한다. 따라서 우리가 원하는 적절한 모델 복잡도는 두 가지 에러가 모두 낮아지는 지점의 모델인 것이다.

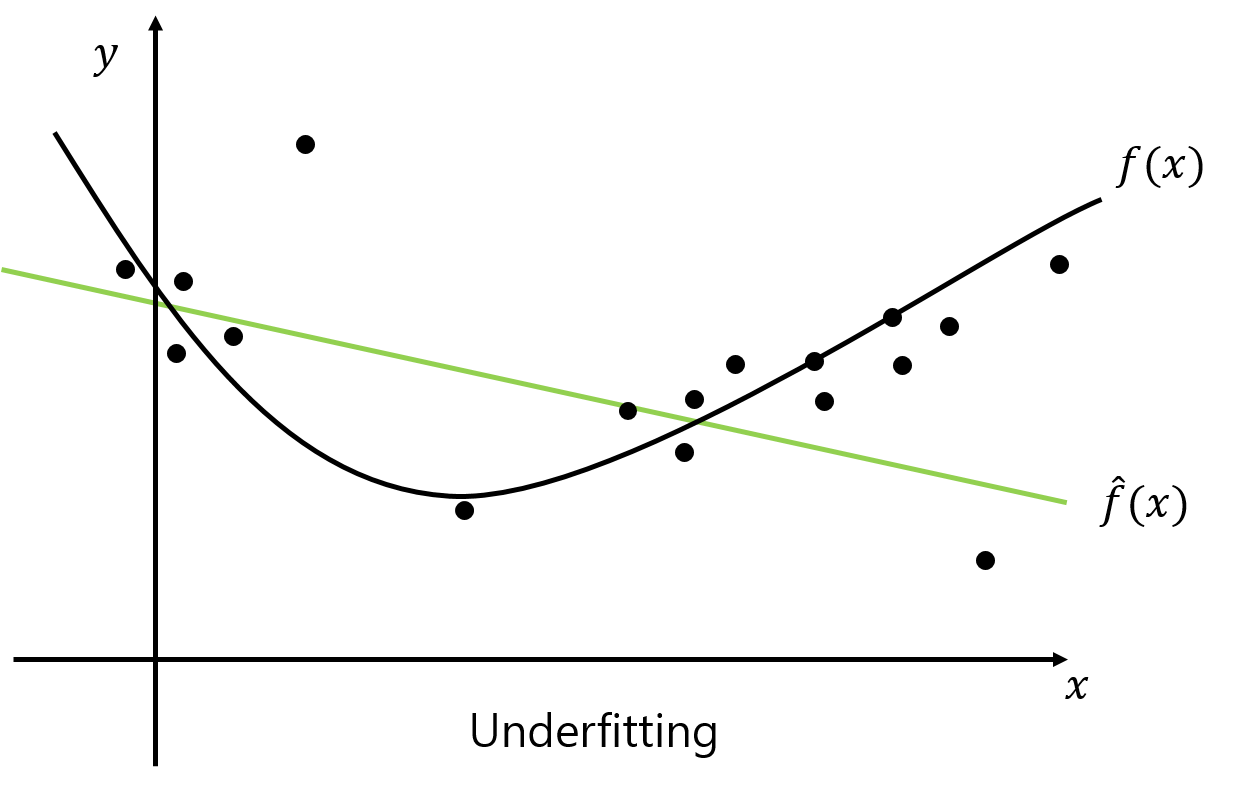
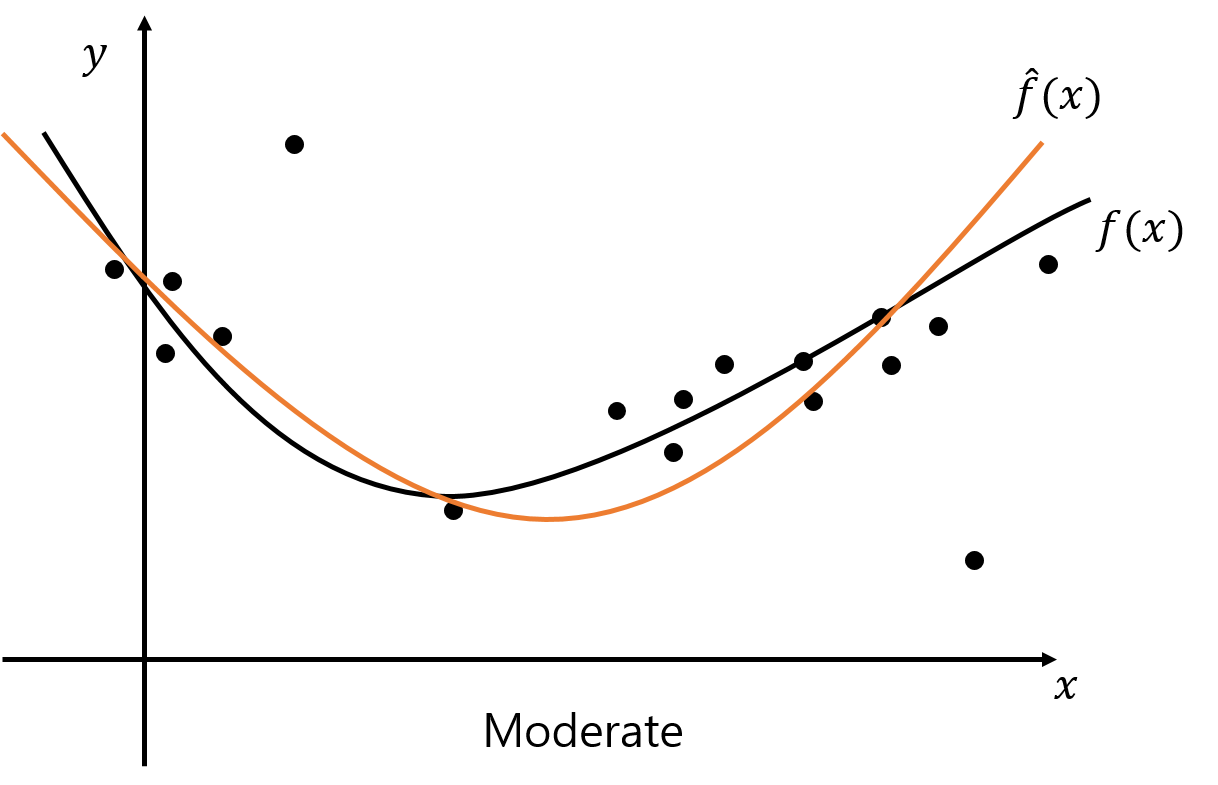
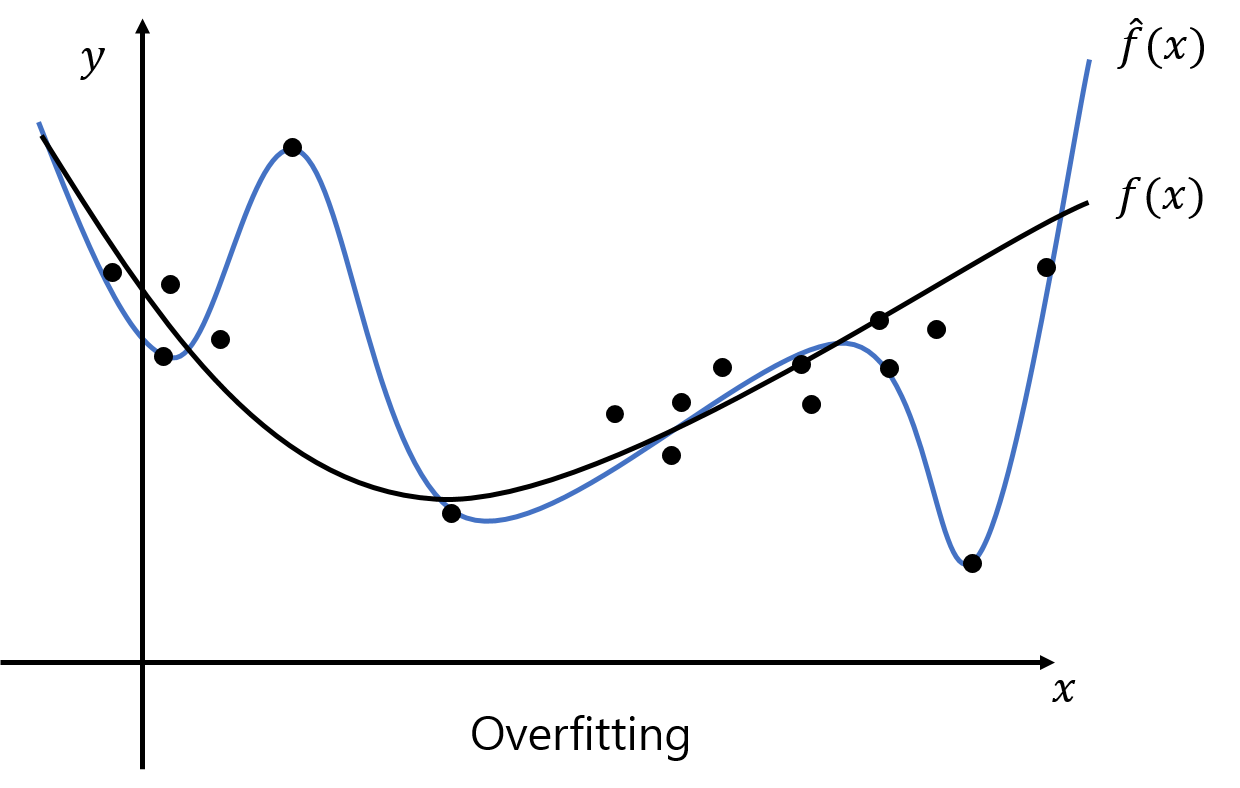
오버 피팅과 언더 피팅에 대해 구체적인 예를 통해 살펴보자. 다음은 2차 함수 형태의 실제 모델 $f(x)$와 그 샘플링 데이터를 서로 다른 모델 복잡도를 갖는 다항 함수 $\hat{f}(x)$로 학습했을 때의 결과 그래프이다. 검정색 실선과 점은 각각 실제 모델 $f(x)$와 그로부터 샘플링한 트레이닝 데이터를 나타낸다. 트레이닝 데이터로 학습한 $\hat{f}(x)$는 컬러 실선으로 표현되었다.

낮은 모델 복잡도	적정 모델 복잡도	높은 모델 복잡도
Underfitting	Moderate	Overfitting

위의 그림에서 점들 (트레이닝 데이터)과 $\hat{f}(x)$와의 차이는 $E_{train}$, 검정 실선과 컬러 실선의 차이는 $E_{test}$를 의미한다. 첫번째는 2차 함수 형태의 실제 모델 $f(x)$를 모델 복잡도가 그보다 낮은 1차 함수로 모델링하는 상황으로 언더 피팅이 발생. 두번째의 경우 $\hat{f}(x)$ 또한 2차 함수이므로 트레이닝 / 테스트 에러가 모두 낮은 이상적인 상황이다. 마지막으로 $\hat{f}(x)$를 고차 다항식으로 설정했을때의 학습 결과인데, 샘플링한 모든 점과 가깝게 지나기때문에 트레이닝 에러는 매우 낮게 나오지만 $f(x)$와의 차이는 오히려 큰 폭으로 증가한 오버 피팅이 발생한 상황이다.

결과적으로 오버 피팅과 언더 피팅이 발생하지 않는 적절한 모델 복잡도를 갖도록 설계해야한다 (닭 잡는데 소 잡는 칼은 필요없다.). 하지만 다시 학습하려는 실제 모델을 모른다는 원래의 문제점이 튀어나온다 (하지만 뭘 잡게 될지 아직 모르는 상황!!). 만약 알고있다면 이러한 문제로 고민할 이유가 없다.

기계 학습의 본질은 결국 실제 모델을 모르는 상황에서 경험적인 데이터를 통해서 자동적으로 모델을 학습, 유추하는 시스템이기 때문이다. 또한 적절한 모델 복잡도란 학습하려는 실제 모델에 따라 상대적인 것이므로 오버 피팅이란 생각보다 까다로운 문제인 것이다.

3. Regularization

결과적으로 적절한 모델 복잡도를 한번에 찾을 수가 없기 때문에, 오버 피팅/언더 피팅을 방지하기 위해 남아있는 두가지 선택지가 남는다.

1. 낮은 모델 복잡도에서 출발하여 모델 복잡도를 증가시키면서 찾는 방법.
2. 높은 모델 복잡도에서 출발하여 모델 복잡도를 감소시키면서 찾는 방법.

그렇다면 우리는 어떠한 전략을 취해야 효과적일까? 사실 두가지 전략 모두 적합하지 않다고 본다. 그 이유는 인공 신경망에서 모델 복잡도를 바꾼다는 것은 결국 새로운 모델을 학습해야 한다는 것을 의미한다. 간단한 모델이야 쉽게 변경해가면서 테스트 해볼 수 있겠지만, 복잡하고, 대량의 데이터에 적용하는 경우는 매번 복잡도를 바꿔가며 학습한다는 것이 물리적으로 어려운 일이다.

따라서 이러한 문제를 해결하기위한 전략이 바로 Regularization이며, regularization은 네트워크가 높은 모델 복잡도를 갖지만 이에 대한 제약을 거는 방식으로 동작하게 된다.

1. 학습 데이터의 부족
2. 데이터 대비 높은 모델 복잡도