Wasserstein Auto-Encoders
2018 / ICLR 2018 / Ilya Tolstikhin, Olivier Bousquet, Sylvain Gelly, Bernhard Schoelkopf
본 논문은 ICLR 2018 top 100 논문 중 하나입니다.
- Section 3, Supplementary는 내용은 수정 중입니다.
- 잘못된 해석 + 번역이 있을 수 있습니다.
1. Introduction
Generative model의 주요 모델로 VAE와 GAN이 있다. VAE는 이론적인 접근방법이 잘 구성되어있으나, 이미지 생성시 blurry한 샘플을 생성하는 단점이있다. 반면에 GAN에서 생성하는 이미지들은 시각적으로 잘 구성된 이미지들을 생성하지만, encoder가 존재하지 않는다 (따라서 주어진 데이터로부터 latent variable $z$를 뽑아낼수 없다). 또한 상대적으로 학습이 어렵고, “Mode collapse” 문제가 발생한다. 따라서 GAN의 구성뿐만아니라 VAE와 GAN을 융합하려는 다양한 연구들이 있었다.
본 논문은 optimal transport (OT) 관점에서 generative model을 분석하여 ($\text{OT}\ \it{W}_c(P_X,P_G)$를 최소화하는 문제) Wasserstein Autoencoder (WAE)를 제안하였다.
- True data distribution : $P_X$
- Latent variable model : $P_G$
- Prior distribution : $P_Z$
- Generative model of $X$ given $Z$ : $P_G(X\mid Z)$
저자가 이야기하는 본 논문의 컨트리뷰션은 다음과 같다.
- 어떠한 cost function $c$에 대한 Optimal transport $(W_c(P_X,P_G))$를 최소화하는 형태의 새로운 regularized autoencoder인 WAE 제안.
VAE의 ELBO와 유사하게 objective function은 $c$-reconstruciton cost와 regularizer $\mathcal{D}_Z(P_Z,Q_Z)$로 구성되어있다.
특히 $c$가 squared cost이고 $\mathcal{D_Z}$가 GAN objective일때 WAE는 Adversarial autoencoder (AAE)와 일치한다. - MNIST와 CelebA 데이터셋에 대해 squared cost WAE에 대한 empirical evaluation을 수행 (squared cost : ($c(x,y)=|x-y|^2_2$)).
실험 결과를 통해 제안한 WAE가 VAE의 장점들을 수용하면서 (안정적인 학습, 인코더-디코더 구조, latent variable 학습) 생성된 샘플의 품질이 향상된것을 확인 할 수 있다. - 두개의 다른 형태의 regularizer $\mathcal{D}_Z(P_Z,Q_Z)$에 대해 분석하였다. 첫번째는 GAN 기반, 두번째는 maximum mean discrepancy (MMD) 기반의 regularizer이다. 특히 두번째는 adversary없이 최적화가 가능하다는 장점이 있다.
- WAE objective에 대한 이론적인 전개는 초기형태의 $W_c(P_X,P_G)$가 probabilistic encoder $Q(Z\mid X)$의 최적화 문제와 동일하다는 것을 보여준다.
2. Proposed method
본 논문에서 autoencoder 구조를 통해 optimal transport $W_c(P_X,P_G)$를 최소화하는 방법을 제안한다.
VAE와 같은 generative model의 목적은 결국 generator가 생성하는 데이터의 분포 $P_G$를 원래 데이터의 분포인 $P_X$로 만드는 것이다. optimal transport는 $P_G$의 일부를 변형시켜 새로운 $P_{G’}$를 생성 할 때 cost가 발생하면 $P_{G’}$가 $P_X$로 될 때까지 필요한 평균 cost를 알 수 있다. 이 때 $P_G$에서 $P_X$로 변형시키는 방법은 다양하게 존재 할 수있는데, optimal transport는 그러한 평균 cost들의 하한으로 볼 수 있다.
인코더는 상충되는 두가지 목표를 달성하도록 학습된다.
- Ture prior $P_Z$와 encoded distribution of training examples $Q_Z:= \mathbb{E}_{P_X}[Q(Z\mid X)]$의 matching, i.e., $\mathcal{D}_Z(Q_Z,P_Z)$의 최소화
- Training exmaple을 복원하기에 충분히 informative한 latent code $Z$의 학습
위 두가지 목표는 이전에 살펴본 InfoVAE 포스트에서도 reconstruction error와 amortized inference 개념으로 언급되었다.
논문에서는 WAE의 특징을 아래 그림과 함께 설명하고있다.
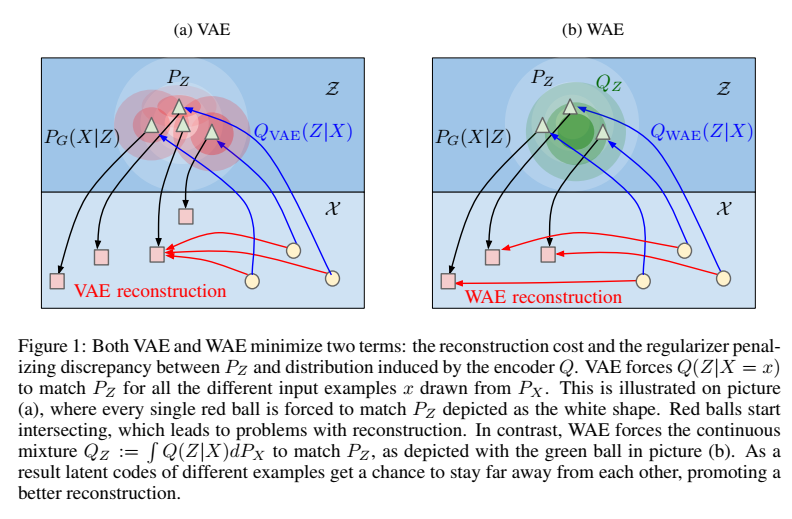 |
| VAE와 WAE의 동작 원리에 대한 비교 |
VAE는 $P_X$로부터 얻는 모든 샘플 $x$에 대해서 $Q(Z\mid X=x)$를 $P_Z$의 형태로 강제한다. 즉, 각각의 삼각형으로부터 생성되는 붉은 원이 $Q(Z\mid X=x)$를 의미하는데, 개별적으로 $P_Z$의 형태 (하얀 원)를 갖도록 만들어진다. (전체 $Q_Z$는 $Q(Z \mid X)$의 합으로 붉은 원이 중첩되는 부분의 확률이 증가하게되고 이로인해 적색 화살표로 연결되는 잘못된 reconstruciton이 발생 할 수 있다.)
반면에 WAE는 개별이 아닌 $Q_Z$가 $P_Z$와 매칭되도록 만든다 ($Q_Z$의 녹색 원이 $P_Z$의 하얀 원의 형태로). 따라서 떨어져 있는 latent code $z$들은 그 reconstruction들도 떨어져있게 된다.
2.1. Prelimniaries and Notations
- Caligraphic letter : 집합, (e.g., $\mathcal{X}$)
- Capital letter : 확률변수, (e.g., $X$)
- $P(X), p(x)$ : 확률 분포 / 밀도 함수
- $f$-divergence : 두 확률 분포의 discrepancy 측정에 사용.
$D_f(P_X| P_G) := \int f(\frac{p_X(x)}{p_G(x)})p_G(x)dx$ $f:(0,\infty)\to \mathcal{R}$는 $f(1)=0$을 만족하는 convex function으로, 대표적인 divergence로 Kullback-Leibler divergence, Jensen-Shannon divergence 등이 있다.
2.2 Optimal Transport and Its Dual Formulations
두 확률 분포의 divergence는 Optimal transport 문제로부터 유도 될 수 있다. OT problem의 Kantrobich’s formulation은 다음과 같다.
\[W_c(P_X,P_G):= \underset{\Gamma \in \mathcal{P}(X\sim P_X,Y\sim P_G) }{\inf} \mathbb{E}_{(X,Y)\sim\Gamma}[c(X,Y)]\]여기서 \(c(x,y): \mathcal{X}\times\mathcal{X}\to \mathcal{R}_{+}\) 는 any measurable cost function 이고 $\mathcal{P}(X\sim P_X,Y\sim P_G)$는 marginal $P_X, P_G$를 갖는 $(X,Y)$의 모든 joint distribution의 집합이다.
특히, $(\mathcal{X},d)$가 metric space이고
Metric space (거리 공간) : $\mathcal{X}$ 내의 두 점 사이의 거리가 distance function $d$로 정의된 공간.
cost function $c$가 distance function에 따라 $c(x,y)=d^p(x,y)\space for\space p\geq 1$ 일 때, $W_c$의 $p$-th root인 $W_p$는 $p$-Wasserstein distance 라 한다. 그리고 $c(x,y)=d(x,y)$일때 Kantrobich-Rubinstein duality가 성립한다.
예를들어 KL-divergence는 대칭성이 성립하지 않기때문에 distance가 아닌 divergence임.
\(W_1(P_X,P_G)=\underset{f\in\mathcal{F}_L}{\sup}\mathbb{E}_{X\sim P_X}[f(X)]-\mathbb{E}_{Y\sim P_G}[f(Y)]\) ($\mathcal{F}_L$ is the class of all bounded 1-Lipschits functions on ($\mathcal{X},d$))
두 거리 공간 $(X,d_X), (Y,d_Y)$ 사이의 함수 $f:= X\to Y$ 와 $K\geq 1$이 다음 조건을 만족 할 때 $f$가 K-Lipschits continuous function 이라고한다.
임의의 $x,x’ \in X$에 대해 $d_Y(f(x),f(x’))\leq Kd_x(x,x’)$ 따라서 1-Lipschits라면 $d_Y(f(x),f(x’))\leq d_X(x,x’)$를 만족한다.
Duality formulation으로 GAN처럼 generator/discriminator 구조로 학습 할 수 있음.
2.3. Application to generative models : Wasserstein Auto-Encoders
VAE나 GAN과 같은 최근의 generative model들은 data distribution $P_X$와 model distribution $P_G$ 사이의 descrepancy measure를 최소화하는 것으로 볼 수 있다. 그러나 기존 논문들에서 보이는 divergence들은 (특히 $P_X$가 Unknown이고 $P_G$가 Deep Neural Network에 의해 parametrized 된 경우) 계산이 어렵거나 불가능하고, 이러한 문제를 해결하기 위해 트릭이 사용된다.
예를들어 KL-divergence의 최소화 (혹은 marginal log-likelihood의 최대화)를 위해서 variational lower bound 가 VAE에서 사용되었다. 좀 더 broad한 $f$-divergence의 경우 dual formulation을 통해 $f$-GAN이나 adversarial training을 활용 할 수 있다. 세번째 옵션으로 본 논문과 같이 OT cost와 Kantrovich-Rubinstein duaility를 활용 할 수 있다.
본 논문에서는 2단계 프로시져로 정의된 latent variable model $P_G$를 다룬다. 2단계 프로시져란 fixed distribution $P_Z$로 code $Z$를 샘플링하는 1단계와, $Z$를 $X\in\mathcal{X}$로 매핑하는 2단계 구성을 말한다. 이는 확률 밀도 함수 $p_G(x)$를 다음과 같이 정의한다.
\[p_G(x):= \int_\mathcal{Z}p_G(x\mid z)p_Z(z)dz, \forall x \in \mathcal{X}\]그리고 문제를 간단하게 하기위해 non-random decoder (i.e., deterministically map $Z$ to $X=G(Z)$)에 대해 진행한다.
이러한 모델에서 OT cost 문제는 복잡하게 $\Gamma$에서 찾을 필요없이 하나의 확률 변수를 통해 더 간단하게 표현 될 수 있다.
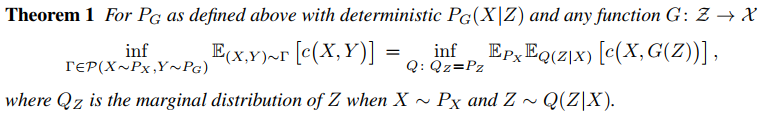 |
Theorem 1은 모든 $X, Y$ 페어 대신 random encoder $Q(Z\mid X)$를 최적화하는 방법으로 OT cost 문제를 해결 할 수 있게 해준다. 추가적인 relaxation과 페널티를 포함한 최종적인 WAE objective는 다음과 같다.
\[D_{\text{WAE}}(P_X,P_G):= \underset{Q(Z\mid X)\in\mathcal{Q}}{\inf} \mathbb{E}_{P_X}\mathbb{E}_{Q(Z\mid X)}[c(X,G(Z))] + \lambda\cdot\mathcal{D}_Z(Q_Z,P_Z)\]$\mathcal{Q}$는 any nonparameteric set of probabilistic encoder, $\mathcal{D}_Z$는 $Q_Z,P_Z$ 사이의 arbitrary divergence, $\lambda$는 0 이상인 hyperparameter이다. Theorem 1의 $Q_Z=P_Z$ 조건이 $D_Z$ 바탕의 penalty term으로 변환됨. 시뮬레이션에서 $c$가 squared distance를 사용했는데, 결국 reconstruction error와 regularization term으로 볼 수 있음.
VAE와 달리, WAE formulation은 non-random encoder의 사용도 허용한다. \(\mathcal{D}_Z\)가 arbitrary divergence이므로 KL-divergence 이외에 것도 사용가능한데, 본 논문에서는 Jensen-Shannon divergence $D_{JS}$와 Maximum mean discrepancy (MMD) 두 모델에 대해 비교하였다.
- GAN based \(\mathcal{D}_Z\) : $D_{JS}(Q_Z,P_Z)$와 adversarial training을 활용. 특히 discriminator가 \(\mathcal{Z}\) space 상에서 $P_Z$로부터의 true sample과 $Q_Z$로부터의 fake sample을 구분하도록 만듬.
- MMD based \(\mathcal{D}_Z\) : Positive-definite reproducing kernel $k:\mathcal{Z}\times\mathcal{Z}\to\mathcal{R}$에 대해 maximum mean discrepancy (MMD)는
\(\text{MMD}_k(P_Z,Q_Z)=\| \int_{\mathcal{Z}}k(z,\cdot)dP_Z(z)-\int_{\mathcal{Z}}k(z,\cdot)dQ_Z(z){\|}_{\mathcal{H}_k}\)
$\mathcal{H}_k$ 는 RKHS (Reproducing Kernel Hilbert Space) of real-valued functions mapping $\mathcal{Z}$ to $\mathcal{R}$. $k$가 characteristic function이면 $\text{MMD}_k$는 metric을 정의하고 divergence measure로 사용 될 수 있다.
각 모델에 대한 알고리즘은 다음과 같다.
|
이전에 논문에서 언급한대로, deterministic encoder $Q_\phi (Z\mid x)$를 사용 할 수 있기때문에 $\tilde{z}_i$를 샘플링 할 때 단순히 출력 값을 넣어주면 된다 (VAE에서는 reparametrization trick을 통해 randomness가 들어간다).
3. Related Work
4. Experiments
실험을 통해 제안된 WAE 모델이 다음의 세가지 목적을 달성하는지에 대해 살펴보았다.
- data points들의 accurate reconstruciton
- reasonable geometry of the latent manifold
- random generated sample들의 good visual quality
논문에서는 MNIST와 CelebA 데이터셋에 대해 실험을 진행했는데, 그 중 CelebA의 결과만 포스팅한다. 실험간에 isotropic Gaussian prior distribution (i.e., $P_Z(Z)=Z;\mathbf{0},\sigma^2_z\cdot \mathbf{I}_d)$), squared cost function $c(x,y)=|x-y{|}^2_2$, deterministic encoder-decoder, Adam optimizer, DC-GAN 논문의 구조와 유사한 신경망 구조, batch normalization 등을 활용했다.
 |
| CelebA 데이터에 대한 비교 결과 |
5. 결론
Optimal transport cost를 활용해 Wasserstein auto-encoder를 제안. 실험을 통해 VAE와 제안된 WAE-GAN, WAE-MMD 모델을 비교, 더 좋은 결과를 얻을 수 있었음.
6. 요약
- Probability distrubtion의 divergence는 Optimal transport 문제로부터 유도 될 수 있고, $c(x,y)=d(x,y)$ 일 때 $W_1=W_c$이며 Kantrovich-Rubinstein duality가 성립함.
- Generative model의 목적은 data distribution $P_X$와 model distribution $P_G$를 같아지도록 만드는 것 (차이를 줄이는 것).
- 물론 두 probability distribution의 차이로 Wasserstein distance 또한 사용 가능.
- 그런데 Optimal transport problem을 살펴보면 $X,Y$의 모든 joint distribution에 대해서 infimum을 살펴봐야하는 문제가 있음.
- $P_G$를 latent variable $z$를 통한 2단계 모델 ($P_Z$에서 $z$ 샘플, 샘플된 $z$로부터 $x$로의 변환)로 구성하면 문제가 간단하게 변함 $\to$ Theorem 1.
- Theorem 1에서 $Q_Z=P_Z$로 constrained되어있으므로 relaxation을 위해 $\mathcal{D}_Z(Q_Z,P_Z)$를 penalty term으로 추가.
- penalty term으로 Jensen-Shannon divergence와 MMD를 사용해서 결과를 비교.

댓글남기기