Mean Squared Logarithmic Error

Mean Squared Logarithmic Error (MSLE)

MSLE의 정의는 다음과 같다.


MSLE	$\frac{1}{T}\sum_{t=1}^T(log(y_t+1)-log(f_t+1))^2$	실제와 예측의 로그값의 오차 제곱의 평균값.

MSLE의 성질.

큰 $y_t$ 값에서 발생하는 오차의 영향을 줄여줌.
ex. $y_t+1=100, f_t+1=110$ 일 때와 $y_t+1=1, f_t+1=11$ 일때 모두 squared error $(y_t-f_t)^2=100$이지만
squared logarithmic error는 각각 0.0017, 1.08임.
즉 $y_t$ 값이 클때 허용되는 절대적인 오차의 범위가 커짐. 이는 위 수식이 $y_t-f_t$인 residual 형태로 보이지만 실질적으로는 mape처럼 비율 기반의 오차이기때문.

Absolute Percentage Error가 $|\frac{e}{y_t}|$ 형태라면 ($e=y_t-f_t$) $log(\frac{y_t+1}{f_t+1})=log(\frac{y_t^*}{f_t^*})=log(1+\frac{e}{f_t^*})$
Underestimate (실측값보다 작게 예측) 보다 overforecast (실측값보다 크게 예측) 더 큰 오차를 갖는다.
MAPE 가 underestimate 되는 것과 반대로 MSLE는 overestimate.
Why? log 를 합치면 $log(y_t+1/f_t+1)$의 분수꼴이 나옴. $a = \frac{y_t+1}{f_t+1}$ 일 때, Underestimate 케이스의 경우 $a\geq1$, overestimate 케이스의 경우 $a<1$.
$(log(a))^2$ 그래프를 그려보면 $a<1$ 구간의 값이 더 큰 것을 확인할 수 있음.
따라서 overestimate가 더 큰 패널티를 갖음.

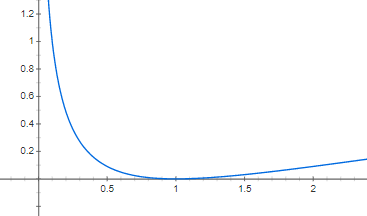squared log(x) 그래프 개형


MSLE	\(\frac{1}{T}\sum_{t=1}^T(log(y_t+1)-log(f_t+1))^2\)	실제와 예측의 로그값의 오차 제곱의 평균값.